코딩 테스트 합격자 되기 : 자바 편 - 9. 트리 (280~301p)
1. 트리 개념
트리(tree) : 데이터를 저장하고 탐색하기에 유용한 구조
트리가 데이터를 저장하고 탐색하는 방식 !
용어 : 원소/노드 /버텍스, 가지/간선/에지, 가중치/웨이트
코딩테스트에서는 이진 트리(binary tree)만 알고 있으면 충분 ! (모든 노드의 최대 차수가 2를 넘지 않는 트리 = 간선이 최대 2개인 트리)
* 트리의 특성을 활용하는 분야 : 계층 구조 표현 (ex. 파일 시스템, 디렉터리 구조 등)
- 인공지능 : 판단 기준 만들 때 의사 결정 트리 사용
- 자동 완성 기능 : 문자열 처리에도 많이 활용 (트라이)
- 데이터베이스 : 데이터를 쉽게 검색, 삽입, 삭제 (B- 트리, B+ 트리)
1) 나무를 거꾸로 뒤집어 놓은 모양의 트리
트리 : 나무 기둥에서 가지가 뻗어나가는 모습을 거꾸로 뒤집어 놓은 모양
-> 나무 밑둥(root)이 맨 위에 있음

* 트리를 구성하는 노드
노드 : 트리를 구성하는 요소
루트 노드(root node) : 노드 중 가장 위에 있는 노드
* 노드를 연결하는 에지
간선, 에지(edge) : 노드와 노드 사이 이어주는 선
트리 : 노드와 노드가 단방향 간선으로 연결 되어 있고, 루트 노드에서 각 노드까지 경로는 유일
레벨 : 루트 노드로부터 특정 노드 까지 거쳐가는 최소한의 간선 수
* 부모-자식, 형제 관계를 가지는 노드
간선으로 연결된 노드들은 서로 부모-자식 관계가 있다고 표현
부모 노드(parent node) : 간선으로 직접 연결된 노드 중 상대적으로 위에 있는 노드
자식 노드(child node) : 아래에 있는 노드
형제 노드(sibling node) : 같은 부모를 갖는 노드
* 자식이 없는 말단 노드
리프 노드(leaf node), 말단 노드 : 자식이 없는 노드
* 아래로 향하는 간선의 개수, 차수
차수(degree) : 특정 노드에서 아래로 향하는 간선의 개수
2. 이진 트리 표현하기
이진 트리 : 노드 하나가 최대 2개의 자식 노드를 갖는 트리
-> 배열이나 포인터로 구현 가능
1) 배열로 표현하기
배열 : 선형 자료 구조, 트리 : 계층 자료구조
-> 배열로 트리를 표현하려면 3가지 규칙 필요
- 루트 노드는 배열 인덱스 1번에 저장
- 왼쪽 자식 노드의 배열 인덱스 : 부모 노드의 배열 인덱스 x 2
- 오른쪽 자식 노드의 배열 인덱스 : 부모 노드의 배열 인덱스 x 2 + 1
-> 단점 : 부모-자식 관계를 곱셈 연산하여 배열의 인덱스로 사용
= 실제 노드 개수보다 많은 공간 사용 (자식이 없거나 쓰지 않는 인덱스 -> 메모리 낭비)
2) 이진 트리 순회하기
순회 : 어떤 데이터가 있을 때 그 데이터를 빠짐 없이 방문하는 것
트리에서 데이터 검색 = 트리 순회

주목해야 할 표현 : 현재 노드를 부모 노드로 생각했을 때,
* 전위 순회 과정 : 부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
트리를 복사할 때 사용
* 중위 순회 과정 : 왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드
이진 탐색 트리에서 정렬된 순서대로 값을 가져올 때 사용
* 후위 순회 과정 : 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 부모 노드 (특성 : 자식 노드부터 방문)
트리 삭제할 때 사용 (노드를 삭제할 때, 부모 먼저 삭제하면 안 되기 때문 / 자식 노드부터 삭제해야 트리를 유지하며 재귀로 루트 노드까지 삭제 가능)
- 방문 : 탐색을 마친 상태 (지나가는 것과 탐색(방문)은 다름!)
3) 포인터로 표현하기
노드는 노드의 값, 왼쪽 자식 노드와 오른쪽 자식 노드를 가짐
배열과 달리 인덱스 연산을 하지 않으므로, 메모리 공간 낭비 x
단점 : 배열로 표현한 트리에 비해 어려움
4) 인접 리스트로 표현하기
정점의 번호(수)만큼 리스트를 만들어야함
리스트는 해당 정점에서 연결된 노드의 번호가 됨
장점
자식 노드의 수가 2개 이상일 경우도 표현하기 좋음
메모리 공간 크게 낭비 x
어떤 정점에서 이동할 수 있는 다음 정점을 빠르게 탐색 가능 -> 시간 복잡도 면에서 상당히 이점이 많음
트리를 포함한 그래프 문제에서 가장 많이 사용하는 표현 방식
3. 이진 트리 탐색하기
이진 트리에서 가장 중요한 것 : 탐색을 효율적으로 할 수 있도록 트리 구축 (= 물건 잘 정리, 쉽게 찾을 수 있음)
1) 이진 탐색 트리 구축하기
이진 탐색 트리 : 데이터 크기를 따져 크기가 작으면 왼쪽 자식 위치에, 크거나 같으면 오른쪽 자식 위치에 배치하는 정렬 방식 가짐
데이터를 전부 삽입한 다음 정렬 x, 데이터를 하나씩 삽입하면서 이진 탐색트리 구축 o (=삽입과 동시에 정렬)
2) 이진 탐색 트리 탐색하기
이진 탐색 트리 탐색하는 방법
1. 찾으려는 값이 현재 노드의 값과 같으면 탐색 종료, 크면 오른쪽 노드 탐색
2. 본인이 찾으려는 값이 현재 노드의 값보다 작으면 왼쪽 노드를 탐색
3. 값을 찾으면 종료. 노드가 없을 때까지 계속했는데 값이 없으면 현재 트리에 값이 없는 것
* 배열 탐색과 비교하면 어떨까?
배열 탐색보다 이진 탐색 트리의 탐색이 빠른 이유 : 이진 탐색 트리의 구축 방식
- 이진 탐색 트리는 크면 오른쪽, 작으면 왼쪽
모든 탐색 알고리즘에서 탐색 효율을 개선하는 방법 : 탐색 대상이 아닌 노드를 한 번에 많이 제외
탐색 대상이 아닌 것들을 빠르게 제외하면 원하는 것을 빠르게 찾을 수 있음
이진 탐색 트리의 구축 방식 : 데이터 크기에 따라 하위 데이터 중 한 방향을 검색 대상에서 제외하므로, 검색을 빠르게 만들어줌
ex. 찾아야하는 수가 루트노드 3보다 크다는 판단 -> 하위의 왼쪽 데이터 : 검색 대상에서 제외
* 이진 탐색 트리의 시간 복잡도
트리 균형에 의존
트리의 균형이 잡혔다 = 각 노드의 차수가 비슷하게 유지되면서 각 노드의 자식 노드 수가 비슷하게 유지 (왼쪽과 오른쪽 서브 트리의 높이 차가 1 이하인 경우)
균형이 유지되었다고 가정했을 때, 삽입과 탐색 연산 시 이진 탐색 트리에 저장된 노드가 N개라고 하면 시간 복잡도는 O(logN)
but. 균형이 맞지 않을 때 -> 시간 복잡도 : 배열과 비슷
3) 이진 탐색 트리와 배열 탐색의 효율 비교
이진 탐색 트리의 균형이 맞지 않으면(최악인 경우), O(N)으로 같다
* 치우쳐진 형태의 트리 (degerate binary tree)
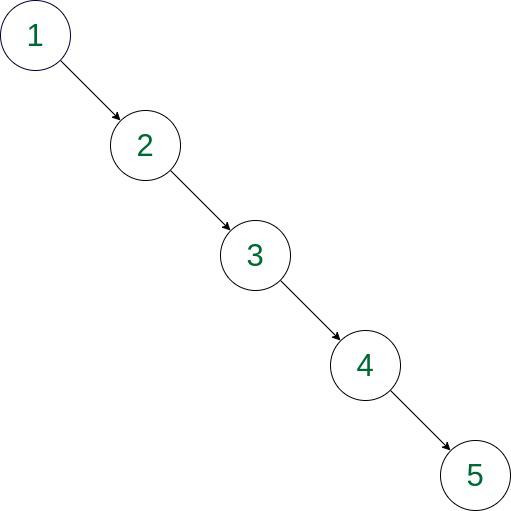
5를 찾는다면 모든 노드를 다 탐색해야 하므로, O(N)의 시간 복잡도 필요
- 균형 이진 탐색 트리 (balanced binary search tree) : 치우쳐지지 않도록 균형을 유지하는 이진 탐색 트리
AVL 트리, 레드-블랙 트리 등
이진 트리의 탐색 연산 횟수가 트리 높이에 비례하고, 트리의 높이는 logN -> 탐색 시간 복잡도 : O(logN)
cf. 구현 난이도 너무 높음
4. 몸풀기 문제
1) 트리 순회*
5. 모의 테스트
1) 예상 대진표*
2) 다단계 칫솔 판매**
3) 양과 늑대*****
4) 길 찾기 게임****